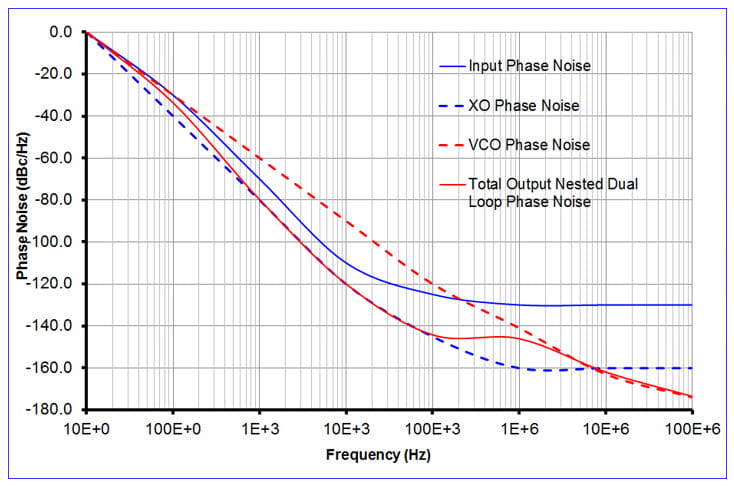
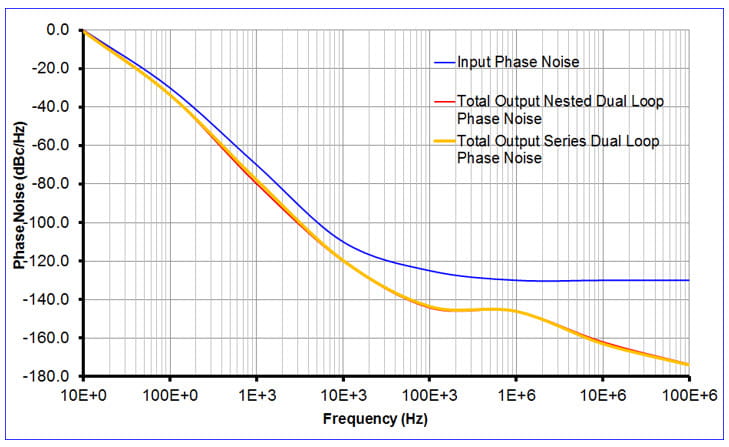
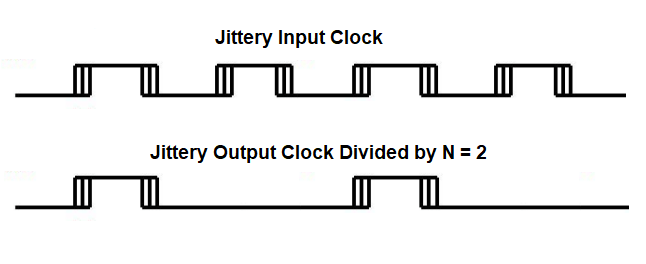
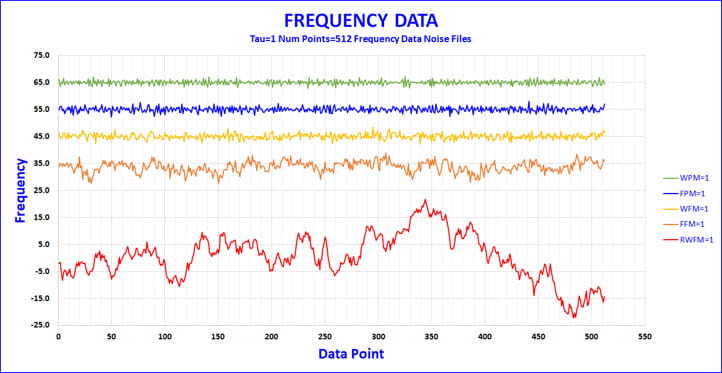
Products
Previously Visited Products
- You have not visited any product pages.
Applications
Previously Visited Applications
- You have not visited any application pages.